Monte Carlo Simulation
This is the process of running any simulation with some form of random numbers in the generation of the simulation algorithm. These types of simulation are not exact, and will have nondeterministic characteristics, therefore needing some sort of statistical error bounds to them.
We might use them where we encounter multidimensional integrals, or systems that involve many different degrees of freedom (e.g., atoms in a gas, solid, liquid, magnets, networks).
Constituent Parts
Monte Carlo simulations include probability distribution functions, some form of random number generation, a sampling rule, some evaluation, and some error estimation.
Estimating Pi Probabilistically
We can do this if we throw darts at the unit square, and measure the proportion of darts that hit the unit circle. The area of the unit square is 1, and the area of the quarter circle would therefore be \(\frac{\pi}{4}\), as \(A = \pi r^2\). and the radius is 1. Therefore the proportion of darts hitting the circle should reasonably well be \(\frac{\pi}{4}\).
The only issue with this is that we don't yet know how to quantify how good the simulation is. We want to know how many trials we need to get an accurate estimate.
Bernoulli Simulation
Let's take every throw as a dart throw with probability \(\frac{\pi}{4}\) for success, then define a random variable for the \(i\)th dart throw as \(x_i=1\) for success or \(x_i=0\) for failure.
The total number \(X = \sum_{i=0}^N x_i\). The estimate then can be defined as \(Y = X/N\). To get the confidence interval, we need some estimation of the variation of the estimator \(Y\). We can then get the standard deviation of \(X\) with the variance of \(x_i\) given as \(p(1-p)\). The variance of \(X\) is then \(Np(1-p)\), as variance is additive. This gives a variance of \(Y ~ 1/N\). Given this, the standard deviation of \(Y\) is \(~N^{-1/2}\). This converges slowly, with the scaling of the decrease of standard deviation with the square of the number of trials.
This method of computing \(\pi\) is very expensive.
Monte Carlo Integration
Recall the numerical integration lecture. The estimates for integrals are of the form \(I = (b-a)/n \sum_i f(x_i)\), taking the function at each interval \(h=1/n\), then adding this all together over the interval \([a,b]\). If we now consider that this is an expectation value of \(\mathbb{E}(f)\) over \([a,b]\), we can start to see how it is more and more similar to the probabilistic estimate.
We can look at estimating the RHS of the equation by taking sample points from \([a,b]\), instead of all the support points. This is the approach used in the darts simulation for the estimate of \(\pi\), and is known as a 'hit and miss' method.
If we now look at the differences between the square method and the new idea we have with the Monte Carlo estimates, we can see the different errors. For the square method, we evaluate the function at \(N\) points, which gives an error \(~1/N\). The Monte Carlo method gives an error \(~N^{-1/2}\), showing that the convergence with the square method is much better than that of the Monte Carlo method.
If we now look at this square method in higher dimensions, as a summation over \(x_1,x_2,\dots,x_d\), we would approximate the integral as:
We'd then need some sort of grid in \(d\) dimensions, and we'd have to space equally, with \(d=20\). Let's day we go fairly coarsely with 5 points per dimension, we get a sum of \(5^{20}\) points. With Monte Carlo, we can just sample randomly, and this would save a lot of computation.
This shows that Monte Carlo is a 'cheap way out' from the sampling methods discussed earlier.
Importance Sampling
For a function that doesn't have a reasonably uniform distribution, such as a normal distribution. The following is not a normal distribution but illustrates the point. It would be good to see that most of the contributions to the function come from the centre, and not the edges of the peak:
To overcome this issue, we can sample non-uniformly by looking at a probability density function \(g(x)\), sampling many data points in the area where \(f(x)\) is large, and proportionally less where \(f(x)\) is small.
So how do we choose \(g\)?
We want to define a function \(g\) such that there is a good ratio of data points that are 'hits' and those that are 'misses'. This can be formalised as follows. If we have a positive function \(g\) with \(\frac{f(x)}{g(x)}\) being quite flat, then the integral of this function between \([a,b]\) can be defined as:
Where the last function listed is a different way of expressing our integral, with \(G(x)\) defined as:
Let's now do a variable change, with \(g\) distributed random numbers, and \(r = G(x)\), then we can modify the equation as follows:
Which is the same integral as above, but more efficiently given as the sampled function is \(\frac{f}{g}\), which is flatter.
Essentially, we want to find a distribution \(g\) such that \(f/g\) becomes flatter. Sampling in this way makes out estimator biased, but this can be corrected by re-weighting.
As usual, there is some trade off between computing costs, as we now need to consider our random number generation. We save costs however, as we sample the more relevant areas of the function, which we give with our random number generator \(g\).
Evaluation via Monte Carlo
If we then start with uniform random numbers \(r\), then the integral becomes:
Importance Sampling Example
Let's try and use Monte Carlo simulation to integrate the function
First, we normalise the function between 0 and 1, which is done with \(g(x)\). This function gives:
To then determine big \(G\), we take the integral between \([0,x]\) of small \(g\) with respect to \(x\):
We can then take the inverse of this big \(G\) to yield our \(u\):
Code Sample
# Seed Random Number
srand();
# Define Quantities
e = exp(1);
sum = 0.0;
# Simulation
for(i = 0; i < N; i++) {
# Select a random number from our function defined earlier
r = -log(1-rand()*(e-1)/e);
fOverG = exp(-r * r)/(exp(-r)*e/(e-1));
sum = sum + fOverG;
}
print(sum/N);
Comparisons of Outputs
If we then run this version of the simulation and compare the results of the direct result (i.e., no biased sampling), then we can see the results and the comparison time. Given the exact result to 6 s.f. is \(0.746824\), we see that the importance result, whilst much slower for a given \(N\), converges much faster to the correct result.
| \(N\) | Direct Sampling Result | Direct Sampling Time | Importance Sampling Result | Importance Sampling Time |
|---|---|---|---|---|
| 10,000 | 0.743275 | 0.20 | 0.746915 | 0.06 |
| 100,000 | 0.746407 | 0.20 | 0.746801 | 0.52 |
| 1,000,000 | 0.746966 | 2.21 | 0.746829 | 4.95 |
| 10,000,000 | 0.746771 | 21.72 | 0.746830 | 48.77 |
Markov Chain Monte Carlo
Generally, we have looked at the use of Monte Carlo methods to allow us to sample from PDFs, and then the use of rejection sampling (hit or miss) and importance sampling. This worked okay in lower dimensions, but as we increase the dimension, it doesn't work as well. The samples were independent, which is what caused the issue in higher dimensions.
Now, we introduce Markov Chain Monte Carlo methods (MCMC), which takes some sample from a random walk, where we explore the sample space by jumping from one point to the next. This means that the samples will be correlated, which is bad in terms of the probability density function. If we generate them correctly, we yield a random walk that will eventually converge to sampling from the desired distribution and this will work better than simple Monte Carlo methods in higher dimensions.
Markov Chains
If we have a state space (continuous of discrete) with states \(x\), the jumps will follow a markov chain, which would look as follows: \(x_0 \to x_1 \to x_2 \to x_3 \to \dots\). Each of these \(\to\) arrows represents some probability to reach a given state \(x_s\) dependent on the immediately previous step. We can thus define the probability of state \(x_s\) as:
Where \(T\) is known as the transition probability. In an uncorrelated system, the transition probability is simply the probability of jumping to a state \(x_s\): \(T = P(x_s) = const\).
To explore using the Markov chain idea, the process as set out needs to be able to reach all the states within the state space. This idea is called ergodicity.
MCMC Algorithm
To generate points from a distribution given with \(f(x)\), with the shape known to some normalisation, we have \(f(x) \propto \rho(x)\), where \(f(x)\) is what we want to sample, and \(\rho(x)\) is real probability distribution.
Initially, we sample uniformly from the domain of the target distribution. We then calculate the PDF at that point, which gives \(\rho(x)\). From here, we can then create a proposal for a new sample by stepping from the current position with some state transition function given as \(x' = x + \Delta x\).
We can then calculate the new PDF value \(\rho(x')\), and the value of \(\frac{\rho(x')}{\rho(x)}\). If the ratio is greater than 1, we accept the step, otherwise if it is less than 1, we can sample a uniform random variable. If the ratio is then greater than the random sample, we accept the step.
If none of this works, then we reject the proposal, adding the current position as a sample, and go back to a new proposal step. The idea of accepting randomly suggested steps with \(\min(1,\rho(x')/\rho(x))\) is quite difficult to justify mathematically, but intuitively, the model of random walks has some chance of visiting states with smaller probability (so we can go back).
States with a larger probability tend to be visited more often and so the probability of visiting different states seems to be proportionate to the probability of that state.
Convergence
We now need to see how we converge with this algorithm. To ensure we converge to a stationary distribution, and to ensure reversibility, we define the probability of jumping from \(x\) to \(y\) is the same as the probability of jumping from \(y\) to \(x\):
This ensures that the MCMC algorithm is ergodic.
We can further refine the model as a proposal, which is given with \(g(x|y)\), and an acceptance or rejection probability $A(x|y), which we can then use to model the transition probability wholly:
We can then show the detailed balance condition for the Markov chain and ensure that the chain is ergodic and converges correctly to the stationary probability distribution.
The most frequently implemented choice of \(A(y|x)\) is as follows, but is not the only way that it can be implemented:
We still have to tune the jump proposal distribution \(g(x|y)\) as this is a parameter of the method, and needs to match the sampling distribution that we have in mind. Typically, this is done by taking the current state and add a random number from the multivariate Gaussian distribution with the variance \(\sigma^2\). This then means the only parameter to choose is the standard deviation.
As a consequence of this, if \(\sigma\) is too small, we converge slowly, and not enough samples are rejected. However, for a \(\sigma\) too large, we also have a slow convergence, with too many samples being rejected.
Example
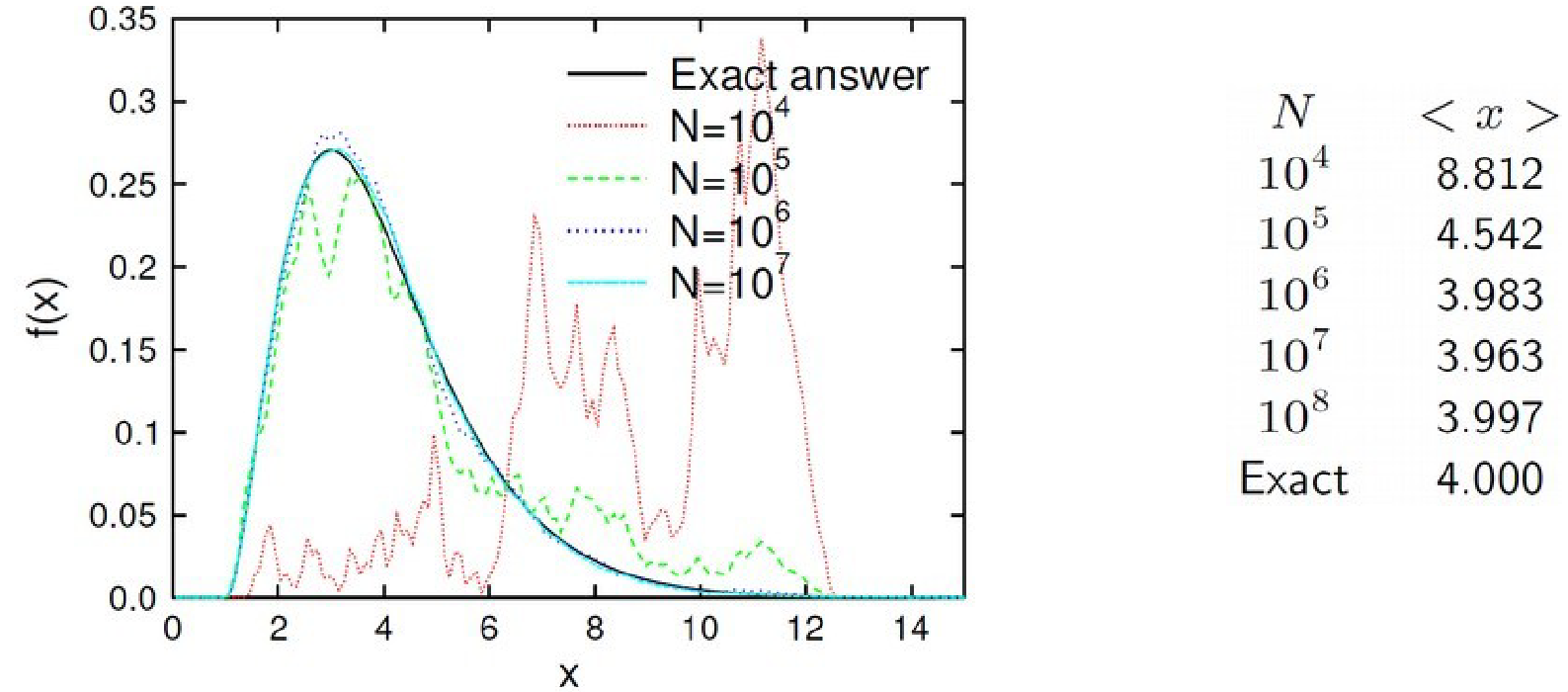
Let's take the function \(f(x)\) as a 1D example:
If we want to sample from this probability distribution and then perform the random walk with varying \(N\), we can see that the average value does eventually converge towards \(4.000\), but needs a high value of \(N\) for this to be the case:
Burn In
MCMC will converge to the distribution \(\rho(x)\) over many iterations. Initially, there is a transient that will not converge, which is an initial transient that must be discarded. To avoid this issue, we run MCMC until the train becomes stationary, then sample over the remaining period after discarding the initial period.
Thinning
Unlike importance sampling or naïve MC, the samples are not independent, as they have a specific dependency on the sample directly before. Therefore, MCMC does not lend itself to standard error analysis, so we must focus on the effective numbers of samples, e.g., by only sampling every \(n\)th point.
Summary
Monte Carlo simulation is any simulation that involves randomness. Where standard integration methods become costly (e.g., in high dimensions, we turn to these MC techniques).
Initial MC techniques involve a uniform sampling from the integrand, but this can be ineffective if the integrand has limited support.
To fix this problem, we use importance sampling and reweight such that the integrand is flat. Furthermore, we introduce the concept of Markov Chain MC, by constructing random walks sampling from the distribution.