Post Quantum
So far, all algorithms discussed have worked with classical computers, which think in terms of regular bits \(\{0,1\}\). For quantum computers, we introduce the notion of quantum bits, or qubits, which we represent with \(Q_0^1\). These qubits can vary in the way they are represented, e.g., as a single photon, a nucleus, or an electron.
For example, an electron spin may have spin-up (↑), or spin-down (↓). We represent those electrons with a spin-up as logical 1, and those with a spin-down as a logical 0. Unlike logic gates on classical computers, and the model of memory and data that we know, qubits can be in an arbitrary combination of different states (i.e., in both ↑ and ↓ simultaneously). We represent this as a qubit \(\ket{w}\) as having two states \(\alpha \ket{1}\) and \(\beta \ket{0}\), where \(\alpha,\beta\) are the probability that the electron is spinning clockwise (logical 1) or anticlockwise (logical 0), respectively:
This is known as superposition. Superposition allows a qubit to perform two calculations at once, and if two qubits are linked through an effect known as quantum entanglement, then we can perform \(2^2\) calculations simultaneously. This continues as we entangle more qubits, to yield \(2^n\) simultaneous calculations.
We can then measure the result, which gets us a single value of the superposition at random, and all other information is lost. The value in quantum computing comes from conversion of the superposition of states into one that contains only the information that they want. A quantum computer is not, therefore, a faster version of a classical supercomputer.
Possible Security Threats
Recall that most modern cryptosystems rely on the fact that either factorising two large integers (factoring problem), or that inverting the exponent of a function (discrete logarithm problem) are both difficult problems to solve.
These problems have, in general, a solution that can only be found in \(e^{O(\sqrt[3]{N})}\) time, which is the general number field sieve. Both these problems cannot easily be computed on a classical computer with classical algorithms, but can be, easily, with Shor's algorithm, with a runtime of only \(O(\ln (N))\) on a quantum computer to decompose a number into its factors.
With access to a quantum computer, an adversary therefore finds it easy to decrypt data that has been encrypted in the past. We are already seeing, through leaked documents, that governmental agencies such as the NSA in the US may be collecting encrypted data for future decryption when they can break the current classical cryptosystems.
Breaking these algorithms would also allow us to forge digital signatures that are currently used to verify the third party.
Grover's Algorithm
If we take a generic search problem:
as a function, with the goal of finding \(x \in X | f(x) = 1\). A classical computer with the best generic algorithm will take \(O(|X|)\), whereas with a quantum computer as per this algorithm, we can get \(O(|X|^\frac{1}{2})\). This algorithm is still a brute force over all the keys, but is still hard for a computer to do. This would effectively halve the security of all algorithms.
To mitigate effects of this algorithm, we simply increase the key size used.
Size of Quantum Computer Required to Break Public Key Cryptography
Luckily, we are standardising all these post-quantum algorithms far in advance of a quantum computer with the necessary power to break them coming about. Current estimates vary but as a rough prediction, we'd need around 10000 logical qubits. A logical qubit requires many quantum logic gates to provide error correction, so we'd need around a billion quantum logic gates to allow for error correction processes.
Development Process of Quantum Computers
We can view the development of a quantum computer as a pyramid, with the most important and useful features on the top, with the underlying techniques to get to these higher-level operations. The development process can be seen in the pyramid below:
Current Quantum Computers
In 2019, Google announced that they had achieved quantum supremacy. This was with the use of a 54-bit Sycamore processor. The task was to sample from a random circuit on 53 qubits, and had no applications.
IBM started in 2019, with 27 qubits, and this has grown steadily to 2023. Currently, their condor computer has 1121 qubits available, and they believe that they can go much, much bigger yet.
When Will Quantum Cryptography Break Public Key Cryptography
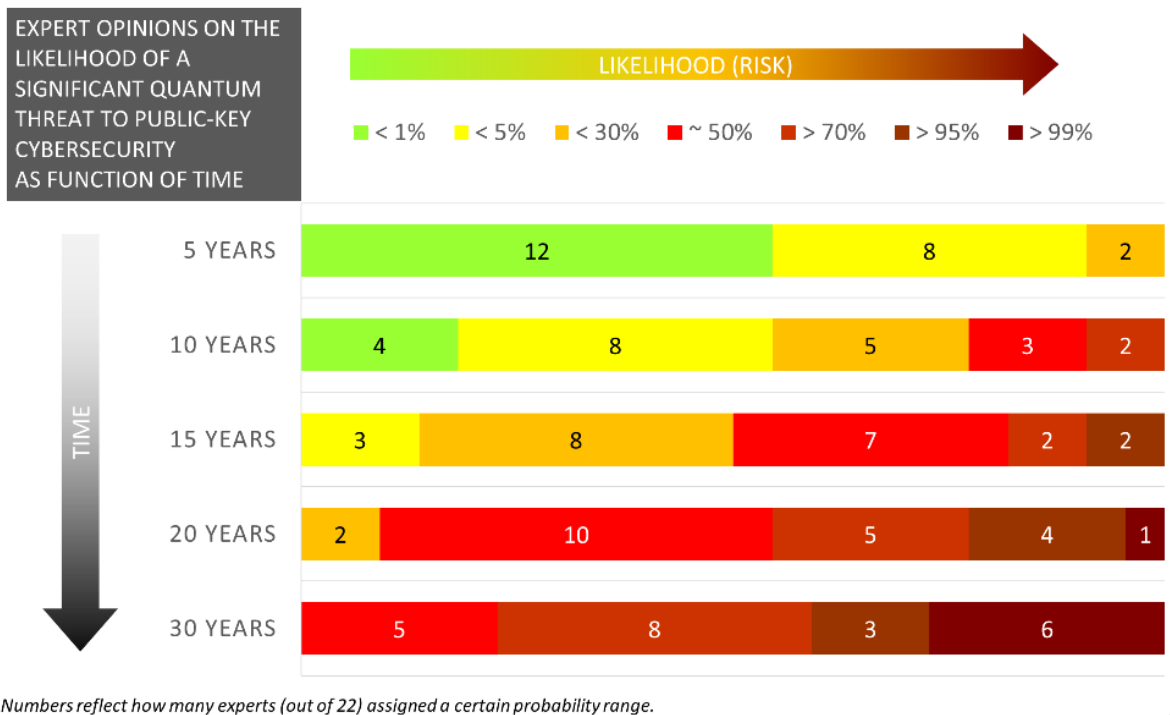
As the future is uncertain and there is no quantifiable law we can extrapolate from (no Moore's law), we can collect the qualitative opinions of experts on the likelihood that a significant quantum threat to public key cryptosystems will exist.
They were asked the risk in terms of a bracketed percentage, which we plot on the \(x\)-axis, and a timescale in 5, 10, 15, 20, and 30 years from now:
Principles of Quantum Safe Cryptosystems
Standardisation by NIST
The NIST process for arriving at quantum-safe algorithms is similar to their process for SHA, AES, etc. They want to ensure these systems are secure as these are the algorithms used by government and military. In the case of quantum, different algorithms have different performance characteristics.
There is unlikely to be a one-size-fits-all algorithm, so NIST accept proposals for algorithms targeting different features. The process for QC is as follows:
- 2016: Start of competition announced
- 2016: Formal call for proposals
- 2017: Deadline for submissions (82 proposals)
- 2017: Round 1 begins (69 proposals)
- 2018: 1st PQC Conference Held
- 2019: Round 2 Begins
- 2019: 2nd PQC Conference Held
- 2020-2022: Round 3 begins, or algorithms selected
- 2022-2025 onwards: draft preparation
As of the slides compilation date in 2023, they were only at the 2022 outcome, where the round 3 algorithms were selected. At this point in time, the only key exchange algorithm was CRYSTALS-KYBER, and 3 digital signatures algorithms: CRYSTALS-DILITHIUM, FALCON, and SPHINCS+.
In addition to these, there are also alternatives, including BIKE, Classic MCEliece, HQC, and SIKE (which has already been broken).
Standards Propagation
Initially, NIST define the standards for the algorithms, or the theoretical way that these algorithms work, the key sizes, etc. After this, the IETF and ETSI define the protocol standards to use these algorithms with. This will ensure interoperability between different implementations and provide the technical implementation details for vendors to follow.
Once this has been completed, vendors can then work to the technical standards for implementation of quantum algorithms in their products. Standards can sometimes be ignored in the process, for example, Signal uses a layered model with an implementation of the CRYSTALS-Kyber protocol on top of their existing ECC encryption standards.
Crystal Kyber
The security of this algorithm is based on the lattice problem. A lattics is a collection of points in an \(n\)-dimensional space that are arranged in a regular pattern. These points can be generated by adding a combination of a set of vectors, forming the basis of the lattice (e.g., \((v_1,v_2)\)). We define these basis vectors as:
Which is a set of linearly independent basis vectors (i.e., \(\forall b_i,b_j, i \ne j \in B, a \in \mathbb{R}, b_i \ne ab_j\)). We can then define the corresponding lattice as:
So a lattice is a set of integer linear combinations, not any arbitrary fractional combination. We then define the minimum distance of the lattice as:
TODO add in what the \(||\) means.
For the same lattice, there may be many different bases, with some vectors short and orthogonal, and some long and acute. The intractable problem that we make use of for security is that given an \(n\)-dimensioned lattice with \(n\) basis vectors, we want to find the shortest non-zero lattice point TODO what is this. This is trivial if we have the right basis vectors, but is very difficult without.
The second mathematical property we can use is that given some basis for a lattice and a target point \(P\) in the space but not a point on the lattice, we want to get the closest lattice point. Again, this is easy to do if we have the \((v_1,v_2,\dots)\), but becomes much harder without.
These are the underlying problems in computing that we use to motivate the algorithm that is being proposed for Kyber. The security of the algorithm is very closely related to the difficulty of solving the shortest vector problem in lattices.
For classic computers, we have \(\approx 2^{2.465n+O(n)}\) difficulty, with only a marginal quantum advantage \(\approx 2^{1.799n+O(n)}\) difficulty. With this, we see that currently, Kyber will remain secure, even with the advent of quantum computing.
McEliece
This is a public key encryption algorithm developed in 1978 by Robert McEliece. This is a candidate for PQC, as it is not vulnerable to Shor's algorithm. The encryption and decryption using these standards is faster than RSA. The main idea is to introduce errors into a data stream that cannot be detected and corrected unless we have the right decoding algorithm.
Given a datastream with length \(n=1024\) bits, with \(t=50\) errors, then the errors can appear in \({1024 \choose 50} = 10^{85}\) possible locations. If we have a fast computer that can try each of these locations in 1ns, it will still take \(10^85 \times 1 \times 10^{-9} = 1 \times 10^{75}\) seconds, which is infeasible (bear in mind the universe is only \(4.3 \times 10^{17}\) seconds old).
Important Distinctions
We need to remember that QCs are not faster supercomputers, and instead perform different calculations by exploiting the superposition state of quantum entities. They are not a near-term threat to the security of PKC, but we must remember that data encrypted now could be stored and attacked later, and that systems may be deployed now and left in operation for 10s of years.
As has been seen already, the transition from old to new algorithms will take some time to complete.
Well done, you've reached the end of my cryptography notes. Pat yourself on the back, take a short break, and get back to revision!