Message Authenticity and Digital Signatures
So far, we have focused on the privacy of messages sent between two persons, and not focused on ensuring that the message is unaltered. Message authentication codes (MACs) are used in this context to ensure the integrity of a received message.
What is Message Integrity?
This is the concern about the message being received and originating from an intended party, without modification from an attacker controlled channel.
We have previously seen error-correction techniques, but these are for integrity of the transmission and do not aid in our confidentiality goals, as error correction codes are easily generated by anyone with the algorithm, so an attacker can alter a message then recompute the error correction code.
Message integrity can be used in operating systems to prevent viruses, or to aid in the integrity of a banking transaction. In an OS, we have software running and we want to check that some virus hasn't amended the system files for the software.
Privacy vs Integrity
Privacy and integrity are different concerns, and it is possible to have one without the other. For example, a message can be signed whilst being transmitted in the clear, or encrypted but without a signature to verify the message integrity. In general, encryption doesn't provide integrity.
Message Authentication Codes
Message authentication codes have two algorithms: a signing algorithm, which takes a message input \(m\) and a key \(k\), to give some sort of tag \(t\); and a verification algorithm which can take some key \(k\), a message \(m\) and the tag \(t\) as inputs, then either accept or reject the message.
Formally:
We then have a consistency condition, as with wrapping an encryption method with a decryption method:
The signing algorithm requires the use of some asymmetric algorithm with a public and a private key, for verification of a third party should we hold their key, or a symmetric algorithm, for verification of messages sent over a clear channel, where both parties have derived a secret key, through e.g., Diffie-Hellman or pre-shared keys.
MAC Security Definition
The adversary's power is in a chosen message attack. If a person creates some \(t\) given some \(S(k,m)\), then they transmit the message and the tag, then for some third party to alter the message \(m \to m'\) and \(t \to t'\), but still keep the verification algorithm working, then the security of the system is flawed. We therefore say that a MAC$ = (S,V)$ is secure if for all efficient \(A\):
We can introduce the notion of forgery as an attacker being able to produce a pair \((m',t')\) such that \(m'\) did not originate from the sender, yet \(V(m',k,t') = 1\). This pair is then said to have been forged.
The chosen message attack is then where the attacker can induce the sender to authenticate messages of the attacker's choice. Therefore, our goal is that we have existential unforgeability. A message authentication code is secure iff the MAC is able to detect any attempt by the adversary to modify the transmitted data.
The attacker should never be able to produce a new \((m,t)\) pair or produce a new tag for an old message.
Example
Is \((S,V)\) such that \(t = S(k,m)\) is always 6 bits long. Is this a secure MAC against a chosen message attack?
As the keyspace for the tag is only \(2^6 = 64\) bits long, then we can simply change the message enough such that we get the same tag. Therefore, this is not secure.
Replay Attacks
These types of attacks are when an attacker re-sends old messages with valid tags. These types of attacks are not prevented by MACs, and an additional stateful mechanism, such as a nonce, or a timestamp need to be used to ensure that a duplicate message will be considered invalid. It is then up to the application to manage the state introduced with the nonces to make sure a message cannot be re-sent.
PRPs and PRFs
Recall from earlier lecutres that a PRF is a pseudorandom function over \((K,X,Y) | F: K \times X \to Y\), giving an efficient algorithm to evaluate \(F(k,x)\).
PRPs, or pseudorandom permutations are a subclass of this, and are defined over \((K,X)\), such that \(E : K \times X \to X\), and there is an efficient deterministic algorithm to evaluate \(E(k,x)\), the function \(E(k, \cdot)\) is one-to-one, and there is an efficient inversion algorithm \(D(k,y)\).
For MACs, we want to use PRFs as we do not want to be able to extract the input text for the function. We can use, for example, AES-128 to construct a MAC for a message.
Example
Suppose \(F: K \times X \to Y\) is a secure PRF, \(Y = \{0,1\}^8\). Is the derived MAC a secure MAC system?
In this instance, the keyspace for the tag is only 8 bits, or 256 possible combinations. Therefore, we can easily bruteforce this system, so it is not secure.
Tag Generation
For long messages, we want to be able to generate a tag. There are two main constructions we can use in practice: ECBC-MAC (used in banking), and HMAC (used in internet protocols).
Both these protocols take a small MAC and convert it into a big MAC.
TODO difference between small and big MAC.
ECBC-MAC
If we let \(F: K \times X \to X\) as a PRP, with \(m\) a long message in \(q\) segments \(m[0],m[1],\dots,m[q-1]\), then the MAC is:
TODO add image
Notice the use of two keys. At the last step, the function uses a second key, as otherwise we have a message that can be chained at the end, given some block we already have the key for.
Attack
The adversary chooses a one block message \(m \in X\). They request the tag for \(m\). They get \(t = F_{RCBC}(k,m)\). They can then output \(t\) as a forgery for the 2 block message \((m, t \oplus m)\).
This forgery can be proved:
Hash-based Message Authentication (HMAC)
This is another way we can construct a MAC for variable length messages, and is implemented the most widely on the internet. These make use of hashing functions.
Hash Functions
Hash functions take arbitrary length inputs and map them to a short, fixed-length 'digest', which is the output. Mathematically, they are defined as:
Hash functions can have different properties based on what they are used for. For example, some hashing functions are used to store passwords, and these need to be hard to reverse, including salts and a number of rounds to make the hash hard to compute computationally.
Security Requirements
First, we define the notion of a pre-image. If \(y = H(x)\), then we say that \(x\) is a pre-image of \(y\). As the size of the output space is typically smaller than that of the input space, we say that each hash value will have multiple pre-images.
We also define the notion of a collision, which is a pair of distinct inputs with the same digests, or mathematically as a pair of inputs \(x,x' | H(x) = H(x')\).
If hashes are being used for secure applications, they need to maintain the following two properties: they are pre-image resistant, meaning it is computationally infeasible to find a pre-image of a hash value; and that they are collision resistant. This means that it is computationally infeasible to find a collision.
Applications
Hashes can be used in many different areas. Commonly, they are used to build message authentication codes, create one-way password files, and for intrusion detection and virus detection by creating and storing hashes of the files on the system, then looking for any changes in these hashes.
Example
If we let \(H: \{0,1\}^N \to \{0,1\}^8\), with a message \(X = (x_0,x_1,\dots,x_N-1)\), and define the hash function as the addition of all these values of bytes (XOR), then is this secure?
Based on the key space only being 256 bits, we can very easily brute force all these possible combinations of outputs by creating our own message then replacing some bytes within the message until we get a collision.
We can show an inverse very easily for the hash function, and show that we can yield a collision by either adding a byte of all zeroes or modifying two bits in the same location in two different bytes such that both bits flip. This will yield the same hash function.
This was a question asked in an exam paper a few times.
Making Hash Functions Collision Resistant (Merkle-Damgard Scheme)
This is a scheme that we can use to get a hash of a message. We break the message into blocks of a fixed size \(K\), then append the last block of the message with some padding if it is smaller than \(K\) (i.e., \(M \mod K \ne 0\)).
If the block is a multiple of \(K\), then we add another block of all padding. The padding bits contain a series of \(1000\), which means that we have reached the end of the message.
We fix the initial vector of the hash function, then combine that with the first block of the message to get the new vector. This is then fed into the hash function with the second part of the message, chaining onto the end of the previous part of the message. At the end of the message, we take the final vector that is the output from the tree, and get the result of the hashing function.
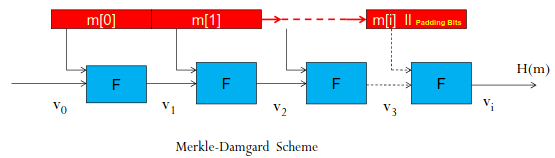
We have a theorem (no proof in the lecture, not expected to know), that states if \(F\) is collision resistant, then \(H\) is also collision resistant.
Collision Resistant Compression Function
This is the Davies-Meyer compression function. If we consider a block cipher \(E : K \times \{0,1\}^n \to \{0,1\}^n\), then the compression function is constructed as:
Where \(F\) is the compression function, taking a vector and the message. TODO what are the other bits it takes.
Secure Hash Algorithm (SHA)
This was an algorithm jointly designed by NIST and the NSA in 1993. It was then revised to SHA-1 in 1995. There was then a version in 2002, which included 3 additional versions of the hashing algorithm: SHA-256, SHA-384, and SHA-512.
These algorithms all give the length of their digest as an output, with SHA-1 having 128-bits.
In 2005, there was a review on the security of the SHA-1 function, as a collision was found using only \(2^{69}\) operations. The structure and details of the newer SHA-2 group of functions are similar to SHA-1, but the security levels of these functions are much higher.
In 2005, NIST began to phase out the approval of SHA-1 as the hashing algorithm of choice.
SHA-256
This algorithm is based on the Merkle-Damgard scheme, with a Davies-Meyer compression function. We have a message \(m_i\) comprising 512-bits, and combine it with the 256-bit block. This is then used with the SHACAL-2 block cipher, and with the Davies-Meyer compression function, we take the output from this scheme and XOR it with the vector to get the vector for the next block.
SHA-3
This is the current version of the SHA standard. Similarly to the competition run by NIST for the symmetric algorithms such as AES, they took requests for proposals in 2007. There were 51 submissions (2008), 14 semi-finalists (2009), with 5 finalists (2010). It was standardised in 2012 with the Keccak algorithm.
The final algorithm is based on sponge construction, which is a completely different structure to that used for SHA-2.
Keyed Hash Functions
Hash functions are used to construct the message authentication codes for variable length messages, which produce a fixed size digest. To then achieve authenticity, MACs should include a key along with the message. This means that \(S(k,m) = H(k || m)\).
Formula differs in lecture slides, \(||\) meaning not covered
Original MACs suffered from weaknesses, so we use secure hashing functions which we then authenticate as they are a fixed length for most hashing nowadays.
HMAC Design Objectives
These are given in RFC 2104. This RFS sets out that HMAC functions should use hash functions without modifications, allowing for substitution of the embedded hash function without much rework. The algorithm should preserve the original performance of the hash function without significant degradation.
It should also handle keys in a simple way, and have well understood cryptanalysis of the authentication mechanism strength. The standard specifies the HMAC function as:
TODO again not sure on the notation here
\(o_{pad},i_{pad}\) are padding constants. We can then make use of any hashing function, e.g., MD5, SHA-1, RIPEMD-160, Whirlpool.
Security of MACs from Hash Functions
Collision resistance is necessary for security. If we consider a MAC \(S(k,m) = H(m,k) = t\), then is \(H\) is not collision resistant, \(S\) is insecure under a chosen message attack.
If an adversary finds \(m_0 \ne m_1 | H(k, m_0) = H(k, m_1)\), then asks for \(S(k,m_0) \to t\), then outputs \((m_1, t)\) as a forgery.
Attacks
Hash functions can be brute forced if we compute \(H(x_1), \dots, H(2_{2^n+1})\). This attack guarantees finding a collision in time \(O(2^n)\) hashes.
Birthday Problem
This was covered in COMP1215: Foundations of Computer Science, and helps us find the probability that at least 2 of \(k\) randomly selected people have the same birthday. If we assume that nobody was born on the 29th February, and people's birthdays are equally distributed over the 365 days of the year, then in a room of \(k\) people, we consider \(q\) as the probability that all people have different birthdays:
Then, the probability that two people share the same birthday is:
Birthday Paradox
If we have a set of identically distributed integers of size \(B\), with \(r_1,\dots,r_n \in \{1,\dots,B\}\) as a subset size \(n\) of \(B\), with all elements randomly selected, then we can use the following theorem:
When \(n = 1.2 \times B^{1/2}\), then \(Pr[ \exists i \ne j : r_i = r_j ] \ge 1/2\). Let's prove it yippee!
First, similar to above, we calculate \(q\), which is the probability that all integers have different values. This is:
Then, we have \(p\) as the probability that at least two of them have the same value, substitute in the value for \(q\):
We can then use the property that \(1-x \le e^{-x}\), and put this into the equation:
If \(n = 1.2 \times B^{1/2}\), then:
No proof required for the exam
Birthday Attack
If we let \(H : M \to \{0,1\}^n\) be a hash function, with \(|M| \gg 2^n\), then we choose \(2^{n/2}\) random messages in \(M = m_1m_2\cdots m_{2^{n/2}}\).
We then compute for \(i = 1,\dots, 2^{n/2}\) \(t_i = H(m_i) \in \{0,1\}^n\). We can then look for a collision such that \(t_i = t_j\).
This attack finds a collision in \(O(2^{n/2})\) hashes. A quantum computer is only marginally better, able to find a collision in \(O(2^{n/3})\).
Hash Function Comparison
| Function | Digest Size (Bits) | Implementation Speed | Brute Force Attack Time | Birthday Attack Time |
|---|---|---|---|---|
| SHA-256 | 256 | Fast | \(O(2^{256})\) | \(O(2^{128})\) |
| SHA-512 | 512 | Fast | \(O(2^{512})\) | \(O(2^{256})\) |
| Whirlpool | 512 | Slow | \(O(2^{512})\) | \(O(2^{256})\) |
Digital Signatures
These are additional information on a message which provides the data origin authentication of the signer as the entity that signed the message. It also provides non-repudiation guarantees, in that a digital signature can be stored by anyone who receives the signed message as evidence that the message was sent and who sent it.
This evidence can then be sent to a third party to prove that the first party sent the message and to resolve possible disputes about the contents or origin of the message.
Digital Signature Systems
DSSes consist of a triple of efficient algorithms \((G,S,V)\), where \(G\) is a kay generation algorithm providing a private key at random from a set of possible private keys and their corresponding public key \((pk,sk)\).
\(S\) is a signing algorithm that takes a given message and a private key and produces a signature. \(S(sk,m) \to t\). Finally, we have \(V\) which is an algorithm to verify a message given a public key and a signature, outputting either true or false. \(V(pk,m,t) \to x \in\{0,1\}\)
RSA Digital Signature Scheme
RSA has been used as a asymmetric cryptosystem. It can also be used to generate signatures. The generation algorithm is to choose random primes \(p,q\), then set \(N = pq\). We then choose integers \(e,d\) such that \(ed = 1 \mod \phi N\), then output the publick key as \(pk = (N,e)\), and the secret key as \((p,q,d)\).
The signing algorithm is then for each message \(x\) we compute a signature \(y\):
To verify the signature, for each received message \(y\), we compute the signature as:
Then, if \(y^e = x\), we can output 1, otherwise output 0.
Security of the Scheme
There could be an existential forgery attack. If Bob signed two messages \(y_1 = x_1^d,y_2 = x_2^d\). The signature for \(x_3 = x_1x_2\) can be forges as \(y_3=y_1y_2\). To prevent this, we need to make use of collision resistant hash functions before signing messages.
Non-non-repudiation
Or what about \((Non-)^2\)repudiation, eh?
If Alice orders 100 shares of stock from Bob, then computes a MAC using a symmetric key, then we want to ensure that Alice cannot claim that she did order the stock. Unfortunately, as we are using a shared key cryptosystem, Bob could forge Alice's messages. You can see the problem here. Bob knows Alice ordered the stock, but cannot prove it.
If Alice signs the order with a private key instead, though, then Bob can prove that Alice, or someone with access to Alice's private key placed the order.
If Alice loses this key pair, then we need to have some way to revoke it.